Research Design
A research design is a blueprint describing how to conduct a research project. It is a plan describing which estimates are to be computed, how they are to be computed and how models are to be tested and refined. A good research design is one that identifies all the things that need to be estimated and works out the best way to measure them.
Information Needs
The starting point for creating a research design should be an understanding of which decisions need to be made. Examples of the type of decisions that research is used to address are:
-
- Should a pack of chewing gum change from 10 to 12 pieces?
- Should a vegetable juice replace its glass bottles with plastic bottles?
- Should an airline replace its economy seats with stand-up beds?
- Who is the best Republican candidate for President?
- How many phone plans should a company offer?
- Which of 10 new product ideas should be further investigated?
- Should a company replace its American call centers with call centers in India?
It is rare that research can actually provide a definitive answer to such questions. Rather, it provides data for a business case. For example, research can provide an estimate of the impact of sales that occurs when a pack of gum is increased by two pieces, and this is combined with the company’s cost data to work to create a business case for the change in pack size.
A key thing to keep in mind when working out which business decisions need to be addressed by research is that the more precisely a firm can identify the key decisions, the more precise the resulting estimates will be. A firm that is able to specify that it wants to understand the impact on sales of changing its pack of gum from 10 to 12 pieces has a good chance of conducting research that is sufficiently accurate to help make this decision. However, if the same firm says that it wants to “understand the consumer value equation for gum, in terms of how consumers trade off price, pack size, multi-packs, flavors and health benefits” it will end up with a much less precise estimate of the impact of a change in the number of pieces and thus risks making worse business decisions.[note 1]
Once the relevant business decisions have been identified and a list of things to be estimated has been created, the next step is to create any appropriate models, as these will lead to the identification of further estimates that are required. For example, the figure below shows a model and information needs for a banking study aimed at increasing acquisition and retention. Where the model has not been proposed by the client (which is usually the case), the researcher then needs to create or find useful models. Usually, one or more of three different types of models are required: models of behavior change, measurement models, and decompositions.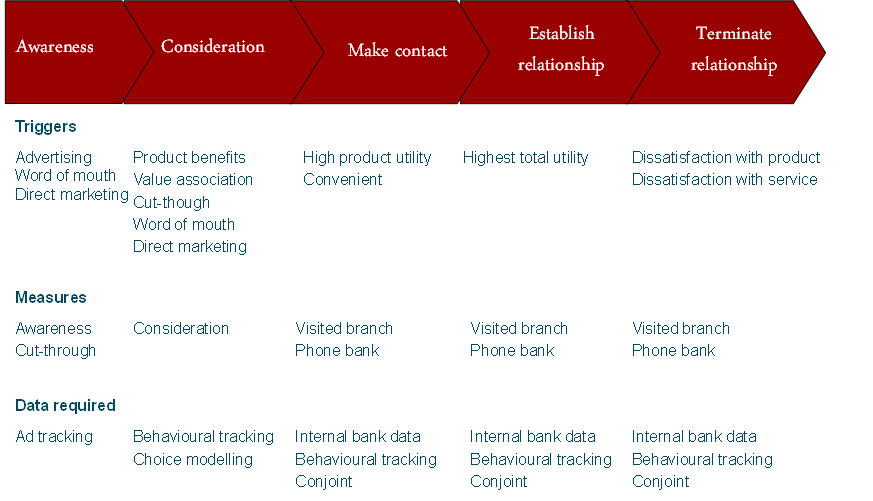
Models of Behavior Change
Research is often desired when a problem has been identified but there is no clear idea of how to solve the problem. For example, a company may wish to identify opportunities for increasing sales. Thus, the behavior to be changed is brand choice, and a model is required which explains what causes this behavior. Although it is possible to conduct qualitative research to try and create such a model from scratch, often models which already exist can be used. For example, when trying to understand how to increase market share, it is common to use a model such as this:[1]
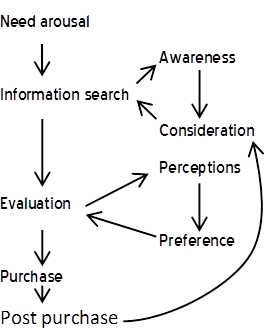
Alternatively, the model may be something much more specific:
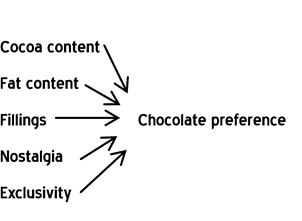
Whatever model is used needs to be able to accommodate the theories and hypotheses that are held by the users of the research. And, it should take into account which outcomes the client is trying to affect (e.g., if the the business objective is to try and reduce the level of defection of its customers, then the model should mention defection as an outcome and have arrows pointing to this outcome).
Experienced researchers often do not write their model down, instead creating it in their heads. Inexperienced researchers often do not know they need to create a model, and instead design their research by repeating aspects of projects they have seen or previously worked upon. Nevertheless, their research is still structured around models. As mentioned, it is impossible to do research without a model. When you do not explicitly create a model, you risk implicitly using an inappropriate model as the basis of your research design.
Decompositions
A decomposition involves breaking something apart. It is a useful way to estimate many things. Let us start with a simple estimation problem. How many Japanese people are there in Australia with dentures (fake teeth that can be taken in and out)? And yes, this was a real-world consulting project.
The simplest and laziest approach to this problem is to do a survey. For example, you might email 1,000 people in Australia and ask how many people in each household are Japanese and have dentures. The result of this would be an estimate of the proportion of Australians that say they are Japanese and have dentures. To get to our required result we would multiply this by the number of Australians. Thus, we have used the following model:
Number Proportion Japanese = Japanese × Number dentures dentures Australians
This formula is a decomposition. We have decomposed the thing we are trying to estimate into two separate estimates – the proportion and the population size.
As research designs go, this is a poor one. The proportion we are trying to estimate is likely to be a very small one (e.g., less than 0.1%). Thus, we would expect that we might need to interview well over 1,000 people before we identified a single one of them and perhaps 50,000 or 100,000 people before we obtained a sufficiently precise estimate, for a cost of millions dollars. People researching bizarre topics are usually short of funds, so we can feel confident that this research design is inappropriate. Furthermore, we probably would not get a very precise answer anyway, as Japanese speakers are relatively less likely to participate. So, how can we resolve this? There are lots of other possible decompositions. For example:
Number Number Japanese = people with × Proporton Dentures dentures Japanese
This decomposition requires two completely different inputs: the number of people with dentures and the proportion of people that are Japanese. Both of these numbers may be available from publicly available sources (e.g., trade associations, government statistics), so we might be able to do this very cheaply. Of course, the result may also be quite inaccurate, because this decomposition implicitly assumes that people of Japanese origin are neither more nor less likely to have dentures than the rest of the population.
So, we can use different decompositions to solve the same problem. The trick is to trade-off which will be cheapest with which will be most precise.
Now, let’s solve a more traditional problem. Consider the problem of trying to predict sales of a new brand of laundry detergent. A standard decomposition for this is:
Sales = Market Share × Market Size
There are lots and lots of ways to estimate market share. One of them is to present people with a screen showing a picture of a supermarket shelf, including the new brand, and ask people to choose one; the proportion of people who choose the new brand is then an estimate of the market share. The market size can usually be obtained from historic sales data.
An alternative decomposition of sales of a new product is:
Intention Sales = to × Purchase × Population purchase frequency size
Intention to purchase is estimated by showing somebody a picture of the proposed new product, and asking them whether they will buy it (this is called Concept Testing). Purchase frequency can be estimated by asking people how many times they will buy it (although looking at historical purchase rates of similar products will often be more valuable). The population size can be obtained from government statistical agencies.
When designing research we need to find the most cost-effective way of producing sufficiently precise estimates. Consider the decomposition of:
Sales = Market Share × Market Size
Let us say we are trying to forecast laundry detergent and we are trying to produce a forecast for next year. To produce our sales estimate we need to estimate market share and market size. It is inevitable that the market size will be broadly similar to the sales from the previous year, with a little growth. So, if the market size last year was $13 billion, the market size next year will probably be between $13 billion and $14 billion.
Now think about the market share estimate. If the new product is a ‘dog’, it will get 0% market share. If it is wonderful, perhaps it can get 20% of the market. So, if we multiply the lower bound estimates of market size and market share we compute a lower bound estimate sales of 0% of $13 billion = $0 and an upper bound of 20% of $14 billion = $2.8 billion. Our range of estimates for market size make comparatively little difference to our forecast. If we assume that the market size is $13 billion, this drops the upper bound from $2.8 billion to $2.6 billion. By contrast, changing the estimated market share from 20% to 0% drops the upper bound all the way down to $0. Thus, the estimate of sales is most sensitive to the estimated market share analysis. This process, of working out which bit of the research design will most impact upon the precision of an estimate, is known as sensitivity analysis. It follows, from this sensitivity analysis, that if we are decomposing sales into market share and market size, our focus in producing an estimate of sales should be on estimating the market share.
Measurement Models
If you have ever watched House or used alternative media, you will be familiar with the idea that people do not always tell us the truth. Expressed in a slightly more academic way: what people say is a mixture of the truth and error:
Observed = Truth + Error
This model is known as a measurement model. And depending on context, it is often described with slightly different terms (e.g., using the terms ‘Measured’, ‘Claimed’, ‘Manifest’ or ‘Estimate’ in place of ‘Observed’). Measurement models are most commonly used in more academic studies. More detail on measurements models is in Measuring Abstract Concepts.
Data Collection Plan
A data collection plan is a document that illustrates the who, what, when, where, why, and how of data collection. This is covered in more detail in the data collection section of this guide.
Analysis Plan
An analysis plan is a list of all the intended analyses that the study will need to address. For example, if the purpose of the study is to work out whether a new product will be successful, then the analysis plan will indicate which analyses will be conducted to answer this question.
Different types of analysis are discussed in the Basic Data Analysis and Advanced Data Analysis sections.
Common things that are usually listed in an analysis plan
- Any particular steps required for data preparation, such as new variables to create, NETs, and weighting.
- The key sub-groups that should be used when exploring the answers to all the questions (e.g., age, gender, heavy vs light buyers).
- Specific analyses that are required (e.g., specific hypotheses to be tested).
Example
The following analysis plan is for a simple Concept Test:
- Create a top two box NET on the purchase intent question.
- Compare the top two box score with top two box scores from similar studies.
- Conduct a Segmentation using the attitude questions.
- Compare top two box scores by segment.
- Code the score’s reasons for liking and disliking the product using the same code frame.
- Crosstab all the questions by:
- Age: Under 30; 30 to 49; 50+
- Gender: Male, Female
- Income: Under $100,000; $100,000 and above

